Глава 28  ◄     Содержание     ►   Глава 30

Three.js и геометрия.   Глава 29.   Триллиант ( Trilliant)

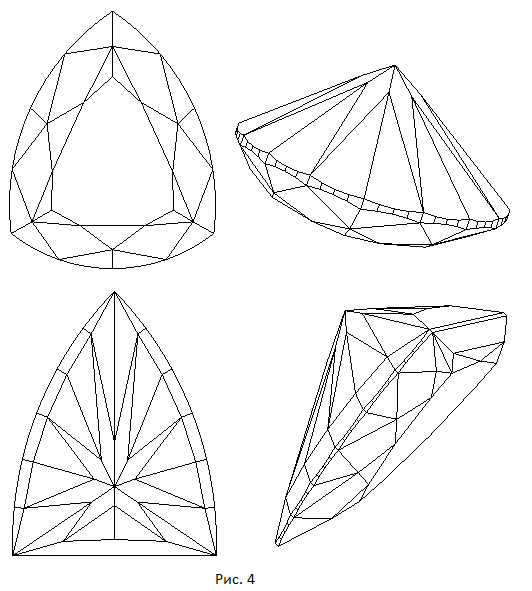
В данном разделе мы создадим модель огранки, которая называется триллиант. В качестве рундиста этой огранки используется рассмотренный в прошлой главе рундист треугольной "подушки".

По ссылке CushionTrilliant A - Light Dispersion можно увидеть эту огранку отображенную при помощи кубических карт. Нажав на приведенной по ссылке странице кнопку Inverse можно увидеть огранку на черном фоне.

Нумерация вершин и обозначение граней модели

Схематичные изображения короны и павильона огранки, а также нумерация вершин показаны на рисунках 1 и 2. Рисунок 1 отображает вид огранки когда наблюдатель находится снаружи модели и смотрит на корону сверху. На рисунке 2 наблюдатель смотрит на павильон сверху как если бы он находился внутри модели.

Структура данных модели (СДМ) огранки

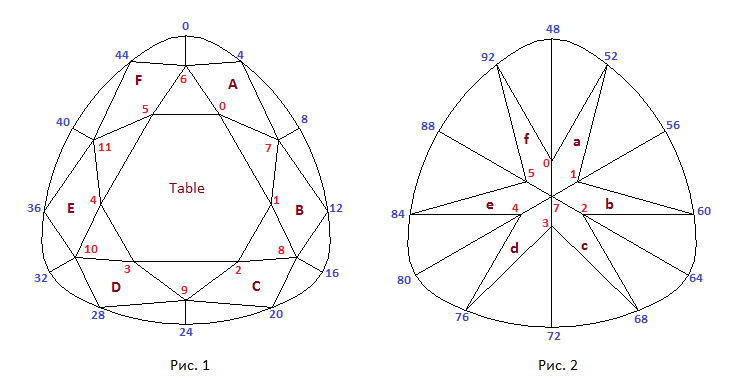
var lw = 1.0;           // отношение длины огранки к ее ширине
// Рундист
var r = 0.06;           // толщина рундиста
var rs = 0.2;           // радиус сопрягающих дуг 
var angle = 60*DEGREE;  // угол задающий положение границ сегментов на линии рундиста

// Корона
var beta = 35*DEGREE;   // угол короны
var t = 0.6;            // размер площадки
var dSquare = 0.0001;   // задает положение вершин короны в горизонтальной плоскости

// Павильон
var angle_pav = 50*DEGREE;  // угол павильона
var hPavFacet = 0.50;       // глубина нижних вершин фасет павильона
// Калетта
var culetX = 0.00001;       // смещение калетты по оси OX
var culetY = 0.00001;       // смещение калетты по оси OY

Расчет положения вершин огранки

Расчет координат вершин рундиста рассматривался в предыдущей главе. Построение короны и павильона в основном подобно этим построениям в огранке бриллиант. Основные части исходного текста расчета координат вершин короны и павильона приведено ниже:

	...........................................................................
	...........................................................................
	// Конструируем корону
	var r_tan_beta = 0.5 * Math.tan(beta); // beta - угол наклона граней короны
	var H1 = r/2;	// уровень верхней части рундиста
	var H2 = -r/2;	// уровень нижней части рундиста

	// точки короны пропорциональны точкам рундиста относительно upPoint (это следует
	// из предположения, что все грани пересекаются в одной точке)
	var upPoint = new Point3D(0.0, 0.0, H1 + r_tan_beta);

	for ( i = 0; i < 6; i++ )
	{
	   var dir = new Vector3D(girdle[i*8+4][0] - upPoint[0], 
	                          girdle[i*8+4][1] - upPoint[1], 
	                          girdle[i*8+4][2] - upPoint[2]);
		// Вектор dir нельзя нормировать !
	    crown[i] = new Point3D(upPoint[0] + t * dir[0], 
	                           upPoint[1] + t * dir[1], 
	                           upPoint[2] + t * dir[2]);
	}

	//  Находим точки пересечения основных граней  
	// короны между собой на уровне рундиста.

	// Сначала создание шести прямых касательных к рундисту
	var lines = [];
	for ( i = 0; i < 6; i++ ) 
	{
	    var dir = new Vector2D(girdle2[4+i*8+1][0] - girdle2[4+i*8-1][0], 
	                           girdle2[4+i*8+1][1] - girdle2[4+i*8-1][1]);
		dir.Normer();
		var ln = new Line2D();
		ln.CreateLineVectorPoint(dir, new Point2D(girdle2[4+i*8][0], 
		                                          girdle2[4+i*8][1]));
		lines[i] = ln;  
	}

	// Точки пересечения касательных к рундисту прямых между собой
	var g2 = [];
	for ( i = 0; i < 5; i++ )
	{
		g2[i+1] = lines[i].IntersectionTwoLines(lines[i+1]);
	}
	g2[0] = lines[0].IntersectionTwoLines(lines[5]);

	// Точки звезды (вершины короны) пропорциональны  точкам g2 относительно upPoint
	// Коэффициент пропорциональности m находим по следующей формуле
	var m = (1 + SQRT2) / 2 * t;
	if ( dSquare <= 0 ) 
		m = m + dSquare * (m - 1 + t);
	else 
		m = m + dSquare * (1 - m);
	// Координаты вершин звезды
	for ( i = 0; i < 6; i++ )
	{
		var dir = new Vector3D( g2[i][0] - upPoint[0], g2[i][1] - upPoint[1], H1 - upPoint[2] );
		var pt = new Point3D( upPoint[0] + m * dir[0], upPoint[1] + m * dir[1], upPoint[2] + m * dir[2] );
		crown[i+6] = pt;
	}
	......................................................................................
	......................................................................................
	//  Конструируем павильон            
	pavil[6] = new Point3D(); 
	pavil[6][0] = culetX;
	pavil[6][1] = culetY;
	pavil[6][2] = - 0.5 * Math.tan(angle_pav)- r/2;

	//  Находим точки пересечения основных граней  
	// павильона между собой на уровне рундиста.
	// На самом деле это те же самые точки из массива g2,
	// которые мы определили при построении короны.
	// Поэтому при построении короны воспользуемся значениями 
	// из этого массива.

	for (i = 0; i < 6; i++)
	{
		var dir = new Vector3D(pavil[6][0] - g2[i][0], pavil[6][1] - g2[i][1], pavil[6][2] + r/2);
	//		dir.normer();
		pavil[i] = new Point3D(); 
		pavil[i][0] = pavil[6][0] - (1 - hPavFacet) * dir[0];
		pavil[i][1] = pavil[6][1] - (1 - hPavFacet) * dir[1];
		pavil[i][2] = pavil[6][2] - (1 - hPavFacet) * dir[2];
	}
	...........................................................
	

Краткое резюме

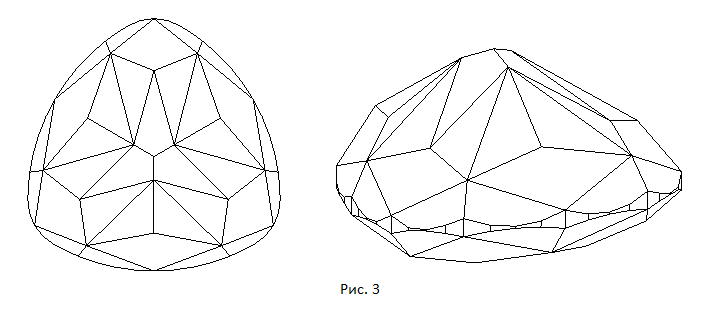
По ссылке Cushion Trilliant B - Light Dispersion можно увидеть еще один подобный триллиант но с павильоном более сложной формы. На рисунке 3 показано изображение этой огранки.

   Глава 28  ◄     Содержание     ► Глава 30