Перейдем к рассмотрению библиотеки WebGeometry используемой для рачета координат вершин 3D моделей.
Oписание всех входящих в нее функций можно найти здесь.
Библиотека включает в себя Javascript функциии для работы с 2D и 3D объектами.
В основном для построения моделей используются трехмерные объекты библиотеки - 3D-точки, 3D-вектора,
прямые в пространстве и плоскости. Но иногда требуются и чисто двумерные объекты - 2D-точки, 2D-вектора,
прямые на плоскости и окружности.
В библиотеке 2D и 3D объекты четко разделены. Отдельно присутствут функции для построений
на плоскости и отдельно для построений в пространстве. Кроме того в библиотеке большую роль играют
функции для работы с матрицами. Для 2D и 3D матриц также присутствуют функции
для обеих размерностей по отдельности. Но функции с матрицами нам практически никогда
не понадобятся, хотя они играют очень важную роль в библиотеке WebGeometry. На их основе
построены функции работающие с точками, прямыми и плоскостями, которые нам требуются в дальнейшем
для построения многогранников.
Начнем с рассмотрения функций библиотеки предназначенных
для работы с 2D объектами. В данном разделе мы рассмотрим на примерах как можно использовать
функции библиотеки WebGeometry применительно к построениям на плоскости.
В показанной ниже программе показано как можно расположить 2D-точку на холсте. При помощи контроллера dat.GUI точку можно перемещать по холсту.
Основная часть исходного текста программы с подробными комментариями объясняющими ее работу:
var elem1 = document.getElementById('canvas_01');
var ctx1 = elem1.getContext("2d");
elem1.style.position = "relative";
elem1.style.border = "1px solid";
/*
// Функции сопряжения координат холста с координатами используемыми в WebGeometry, WebGL и three.js
// Используются внутри функций csp, axes, txt_c (и других ...) для пересчета координат используемых
// в WebGeometry, WebGL и three.js в координаты используемые при построениях на холсте (HTML5 canvas).
function fx(val)
{
var res = val * SCALE + xC;
return res;
}
function fy(val)
{
var res = - val * SCALE + yC;
return res;
}
*/
SCALE = 100; // задает масштаб
xC = elem2.width / 2; // задает положение начала координат по оси OX
yC = elem2.height / 2; // задает положение начала координат по оси OY
// начало координат
var pt00 = new Point2D(0, 0);
// рисуем точку в начале координат коричневым цветом
csp(ctx1, pt00, 2, "Brown");
// обозначаем начало координат символом "O" коричневым цветом
text1(ctx1, "O", pt00, "rt", "up", "Brown");
// рисуем оси коричневым цветом с размахом линий по OX и OY равным 1.8
axes(ctx1, 1.8, 1.8, 0.5, "Brown");
// canvas ctx1
// точка с координатами ( 1.2, -1.2)
var pt0 = new Point2D( 1.2, -1.2);
csp(ctx1, pt0, 10, "B"); // рисуем точку pt0 синим цветом
// формируем строку с координатами точки pt0
var t1 = (roundNumber(pt0[0], 2)).toString(); // преобразование значения в строку
var t2 = (roundNumber(pt0[1], 2)).toString(); // преобразование значения в строку
var t = t1 + ", " + t2;
// отображаем сформированную строку синим цветом
// рядом с pt0 - чуть правее и чуть выше самой точки
text1(ctx1, t, pt0, "rt", "up", "B");
// переменная controller1 используется dat.GUI
var controller1 = new function()
{
this.X = pt0[0];
this.Y = pt0[1];
}();
// Создаем новый объект dat.GUI.
var gui = new dat.GUI({ autoPlace: false });
gui.domElement.id = 'gui';
gui_container1.appendChild(gui.domElement);
var f1_1 = gui.addFolder('Point position');
// используется для изменения координаты X точки pt0
f1_1.add(controller1, 'X', -2.0, 2.0).onChange( function()
{
pt0[0] = (controller1.X); // задаем новое значение координаты X
// так как новое значение координаты X то требуется
// очистить экран
ctx1.clearRect(0, 0, elem1.width, elem1.height);
// перерисовываем экран с новым положением точки pt0
axes(ctx1, 1.8, 1.8, 0.5, "Brown");
csp(ctx1, pt0, 10, "B");
var t1 = (roundNumber(pt0[0], 2)).toString();
var t2 = (roundNumber(pt0[1], 2)).toString();
var t = t1 + ", " + t2;
text1(ctx1, t, pt0, "rt", "up", "B");
csp(ctx1, pt00, 2, "Brown");
text1(ctx1, "O", pt00, "rt", "up", "Brown");
});
// используется для изменения координаты Y точки pt0
f1_1.add(controller1, 'Y', -2.0, 2.0).onChange( function()
{
pt0[1] = (controller1.Y); // задаем новое значение координаты Y
// так как новое значение координаты Y то требуется
// очистить экран
ctx1.clearRect(0, 0, elem1.width, elem1.height)
// перерисовываем экран с новым положением точки pt0
axes(ctx1, 1.8, 1.8, 0.5, "Brown");
csp(ctx1, pt0, 10, "B");
var t1 = (roundNumber(pt0[0], 2)).toString();
var t2 = (roundNumber(pt0[1], 2)).toString();
var t = t1 + ", " + t2;
text1(ctx1, t, pt0, "rt", "up", "B");
csp(ctx1, pt00, 2, "Brown");
text1(ctx1, "O", pt00, "rt", "up", "Brown");
});
Кроме библиотеки WebGeometry в дальнейшем при выводе на холст мы будем использовать некоторое количество вспомогательных функций, исходный текст которых находится в файле canvas2D.js. Они представляют собой небольшую обертку вокруг стандартного API HTML5 Canvas и позволяют вывести на экран точки, текст, прямые и окружности при помощи сокращенной записи. Эти функции в качестве параметров получают координаты не привязанные к холсту (как в HTML5 Canvas), а непосредственно значения получаемые в процессе расчетов с помощью функций входящих в WebGeomrtry. Также большинство этих функций позволяют задать цвет точек, текста, прямых и окружностей, размер точек и толщину линий.
В приведенном выше исходном тексте использовалась только одна функция создания 2D-точки из библиотеки WebGeometry.
Она создает точку с координатами (1.2, -1.2):
var pt0 = new Point2D(1.2, -1.2);
Создадим две прямые и отобразим их на холсте. Первая прямая задается двумя точками (точки обозначенные на холсте как 1 и 2):
var pt1 = new Point2D ( -1.1, -0.8); // черная точка 1 var pt2 = new Point2D ( 1.1, 0.8); // черная точка 2 var line1 = new Line2D(pt1, pt2); // создаваемая прямаяВторая прямая задается своим направлением при помощи вектора, и точкой принадлежащей создаваемой прямой. При помощи функции
IntersectionTwoLines
определяем точку пересечения двух прямых:
var vec = new Vector2D(0.95, -0.2); // вектор синего цвета var pt3 = new Point2D ( -1.0, 0.7); // точка point синего цвета var line2 = new Line2D(); // объявление прямой line2 // назначение прямой line2 требуемых параметров line2.CreateLineVectorPoint(vec, pt3); // определяем координаты точки пересечения прямых line1 и line2 var point = line1.IntersectionTwoLines(line2); // точка имеющая красный цвет
При помощи dat.GUI можно задавать координаты точек 1 и 2
через которые проходит первая прямая и кординаты вектора и точки для второй прямой.
Возможно представляет интерес посмотреть как это все рисуется на холсте. Далее приведен текст функции cross выполняющий вычисления и отрисовку на холсте с подробными комментариями:
function cross(pt1, pt2, pt3, vec)
{
// pt1 и pt2 задают line1
// pt3 и vec задают line2
ctx2.clearRect(0, 0, elem2.width, elem2.height);
ctx2.lineWidth = 1.0;
ctx2.font = "12px Arial";
axes(ctx2, 1.8);
// Создаем вспомогательную прямую лежащую на оси OX
var pt00 = new Point2D(0, 0); // начало координат
var OX = new Line2D(pt00, new Point2D(1, 0));
csp(ctx2, pt1, 6); // черная точка 1
csp(ctx2, pt2, 6); // черная точка 2
var line1 = new Line2D(pt1, pt2); // создаем line1
line(ctx2, pt2, pt1); // отображаем line1 на холсте
// Для отрисовки вектора на экране
// создаем сначала прямую лежащую на векторе
// Переменная vec объявлена вне данной функции и изменяется в dat.GUI
vec.Normer();
var line_vec = new Line2D(pt00, vec);
// Отображаем вектор на холсте.
// Предположим, что он исходит из начала координат и идет в точку с координатами vec.
// В WebGeometry предполагается, что векторы являются свободными и задают только направление.
// Поэтому можем условно привязать вектор к любой точке - в том числе и к началу координат.
vector(ctx2, pt00, vec, "B");
txt_c(ctx2, "vector", vec, "rt", "up", "B"); // отображаем слово "vector"
// При помощи функции Angle библиотеки WebGeometry определяем угол наклона стрелки на холсте
var ang = (line_vec.Angle(OX) + 90*DEGREE);
// Затем рисуем стрелку на конце вектора
arrow(ctx2, vec, ang, 0.4, "B");
csp(ctx2, pt3, 6, "B"); // отображаем на холсте точку pt3 синим цветом
txt_c(ctx2, "point", pt3, "lt", "up", "B"); // отображаем на холсте слово point синим цветом
// Создаем прямую line2
var line2 = new Line2D(); // объявление прямой line2
// назначение прямой line2 требуемых параметров
line2.CreateLineVectorPoint(vec, pt3);
// находим вспомогательную точку pt_temp для изображения на холсте line2
var pt_temp = line2.IntersectionTwoLines(OX);
// прямая line2 проходит через точки pt3 и pt_temp
// отображаем line2 при помощи функции line (смотри в canvas2D.js)
line(ctx2, pt3, pt_temp, "B");
txt_c(ctx2, "1", pt1, "lt", "up"); // отображаем слово "1" на холсте
txt_c(ctx2, "2", pt2, "lt", "up"); // отображаем слово "2" на холсте
var point = line1.IntersectionTwoLines(line2);
csp(ctx2, point, 8, "R");
var t1 = (roundNumber(point[0], 2)).toString();
var t2 = (roundNumber(point[1], 2)).toString();
var t = t1 + ", " + t2;
txt_c(ctx2, t, point, "rt", "up", "R"); // отображаем координаты точки пересечения
// прямых на холсте красным цветом
csp(ctx2, pt00, 8, "B"); // отображаем точку лежащую в начале координат (8 - размер точки в px)
}
В приведенном выше листинге использовались следующие функции библиотеки WebGeometry:
Vector2D
(Vector2D) Normer
Line2D
(Line2D) CreateLineVectorPoint
(Line2D) Angle
(Line2D) IntersectionTwoLines
В качестве типичного примера создадим окружность и прямую и затем найдем точки их пересечения. На холст окружность и прямую отображает следующая программа:
По тексту программы можно посмотреть как используются некоторые функции библиотеки WebGeometry
для отображения на холст прямых, окружностей и т.д. В следующем листинге
в качестве функции определяющей точки пересечения окружности и прямой используется
функция
Intersection_LineCircle.
Эта функция возвращает массив из двух элементов типа Point2D. Эти два элемента массива представляют собой
две точки пересечения прямой с плоскостью.
function draw_line_circle(ctx, O, pt1, pt2, R)
{
axes(ctx, 1.8, 1.8, 0.5, "Brown"); // оси координат
csp(ctx, O, 5, "B"); // центр окружности
var t1 = (roundNumber(O[0], 2)).toString();
var t2 = (roundNumber(O[1], 2)).toString();
var t = t1 + ", " + t2;
text1(ctx, t, O, "rt", "up", "B");
circle(ctx, O, R, 1, "B");
// радиус - прямая со стрелкой на одном конце
var line_radius = new Line2D(O, new Point2D(O[0] + 6, O[1] + 3));
var cir = new Circle2D(O, R); // Окружность с центром O и радиусом R
// определяем место где нарисуем стрелку радиуса
var points = cir.Intersection_LineCircle(line_radius);
if (points == null)
{
return null;
}
var x, y;
// в качестве места для стрелки выбираем где координата Y
// точки пересесечения имеет меньшее значение
if (points[0][1] > points[1][1])
{
x = points[1][0];
y = points[1][1];
}
else
{
x = points[0][0];
y = points[0][1];
}
// точка для стрелки
var point_radius = new Point2D(x, y);
// радиус
segment_arrow(ctx, O, point_radius, 1, 0.2, "Black")
text1(ctx, "R", point_radius, "lt", "dn", "B");
// прямая OX задается для определения угла используемого
// для проведения отрезка со стрелкой на конце примыкающем к окружности
var O = new Point2D(0, 0); // начало координат
var OX = new Line2D(O, new Point2D(1, 0));
// определяем угол
var ang = (line_radius.Angle(OX) - 90*DEGREE);
// рисуем стрелку на конце отрезка
arrow(ctx, point_radius, ang, 0.2, "B");
// задаем прямую line_var пересекающуюся с окружностью
csp(ctx, pt1, 6);
csp(ctx, pt2, 6);
text1(ctx, "1", pt1, "rt", "up");
text1(ctx, "2", pt2, "rt", "up");
var line_var = new Line2D(pt1, pt2); // прямая задается двумя точками
line(ctx, pt2, pt1, -3, 3, 1, "Black"); // отображаем line_var
// находим две точки пересечения
points = cir.Intersection_LineCircle(line_var);
if (points == null)
{
return null;
}
csp(ctx, points[0], 6, "R"); // первая точка пересечения
csp(ctx, points[1], 6, "R"); // вторая точка пересечения
// координаты первой точки
var t1 = (roundNumber(points[0][0], 2)).toString();
var t2 = (roundNumber(points[0][1], 2)).toString();
var t = t1 + ", " + t2;
text1(ctx, t, points[0], "rt", "up", "R");
// координаты второй точки
t1 = (roundNumber(points[1][0], 2)).toString();
t2 = (roundNumber(points[1][1], 2)).toString();
t = t1 + ", " + t2;
text1(ctx, t, points[1], "rt", "up", "R");
}
Создадим две окружности у которых можно менять координаты их центров и радиусы.
Найдем точки пересечения окружностей друг с другом. Они определяются с помощью
функции
Intersection_TwoCircles
var cir1 = new Circle2D(O1, R1); // первая окружность
var cir2 = new Circle2D(O2, R2); // вторая окружность
var points = cir1.Intersection_TwoCircles(cir2);
if (points == null)
{
return null; // нет пересечения окружностей
}
// пересечение есть
...................
...................
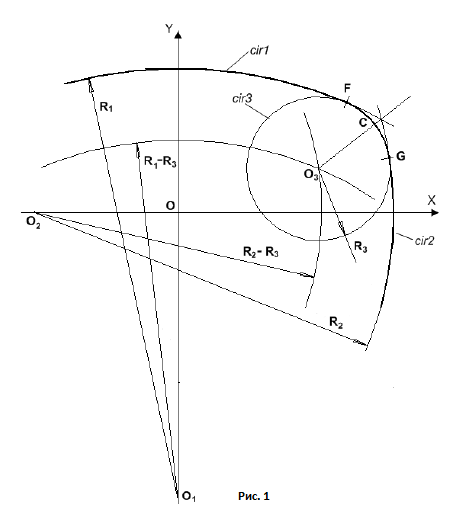
Иногда возникает задача плавного соединения двух окружностей.
Рисунок 1 иллюстрирует это построение. Фактически оно сводится
к сопряжению окружностей cir1 и cir2 дугой третьей окружности cir3.
Окружность cir3 имеет внутреннее касание к окружностям cir1 и cir2
в точках F и G. Термин “внутреннее касание” означает, что центры дуг окружностей
cir1, cir2 и cir3 находятся по одну сторону от точек их касания.
Будем считать, что заданы радиусы R1 и R2 основных окружностей
cir1 и cir2, а также радиус сопрягающей окружности R3.
Предположим также, что известно расположение центров O1 и O2 основных окружностей.
Требуется найти положение центра O3 сопрягающей окружности и координаты точек касания F и G.
Для нахождения центра O3 окружности сопряжения cir3 построим две вспомогательные окружности с радиусами
равными значениям R1 – R3 и R2 – R3. Центры этих вспомогательных окружностей поместим в центры основных
окружностей O1 и O2 соответственно. Тогда центр O3 окружности cir3 можно найти как точку
пересечения вспомогательных окружностей. Для нахождения точек пересечения окружности
cir3 с окружностями cir1 и cir2 создается окружность с центром O3 и радиусом,
отличающимся в большую сторону от R3 на очень малую величину epsilon. Следовательно радиус этой окружности равен
(R3 + epsilon). Введение этой малой величины необходимо для того, чтобы в процессе проведения вычислений заведомо
обеспечить пересечение соответствующих окружностей. В предельном случае, когда значение epsilon стремится к 0,
две точки пересечения сливаются и превращаются в одну точку касания окружностей.
Пересечение окружности cir3 с радиусом равным (R3 + epsilon) с окружностями
cir1 и cir2 даст точки касания F и G.
Точки пересечения окружностей определяются с помощью
функции
Intersection_TwoCircles
Функция отрисовки сопряжения двух окружностей третьей окружностью приведена ниже.
function draw_three_circles(ctx, O1, O2, O3, R1, R2, R3)
{
axes(ctx, 1.8, 1.8, 0.5, "Black"); // рисуем оси черным цветом
// Необходимо провести сопряжение следующих двух окружностей.
var cir1 = new Circle2D(O1, R1);
var cir2 = new Circle2D(O2, R2);
// Рисуем и обозначаем центр O1 коричневым цветом
csp(ctx, O1, 5, "Brown");
text1(ctx, "O1", O1, "rt", "up", "Brown");
// Рисуем дугу с центром O1 и радиусом R1 коричневым цветом
arc(ctx, O1, R1, 1, "Brown", 5, 120);
// Рисуем и обозначаем центр O2 синим цветом
csp(ctx, O2, 5, "B");
text1(ctx, "O2", O2, "rt", "up", "B");
// Рисуем дугу с центром O2 и радиусом R2 синим цветом
arc(ctx, O2, R2, 1, "B", -60, 60);
// Радиусы вспомогательных окружностей должны быть > 0
if (R2 - R3 <= 0.0)
{
return null;
}
if (R1 - R3 <= 0.0)
{
return null;
}
// Создаем две вспомогательные окружности.
var R2_R3 = new Circle2D(O2, R2 - R3);
var R1_R3 = new Circle2D(O1, R1 - R3);
// Две дуги вспомогательных окружностей рисуем черным цветом и толщиной равной 0.3
arc(ctx, O1, R1 - R3, 0.3, "Black", 5, 120); // рисуем дугу с центром O1 и радиусом R1 - R3
arc(ctx, O2, R2 - R3, 0.3, "Black", -60, 60); // рисуем дугу с центром O2 и радиусом R2 - R3
// Находим точки пересечения двух окружностей между собой
// Переменная points представляет собой массив из двух точек типа Point2D.
var points = R2_R3.Intersection_TwoCircles(R1_R3);
if (points == null)
{
return null;
}
// Центр сопрягающей окружности O3
if (points[0][0] > points[1][0])
{
O3[0] = points[0][0]; O3[1] = points[0][1]
}
else
{
O3[0] = points[1][0]; O3[1] = points[1][1]
}
// Создаем сопрягающую окружность чуть большего
// радиуса чем R3 (для проверки)
var cir3 = new Circle2D(O3, R3 + 0.00001); // R3 + EPSILON);
csp(ctx, O3, 5, "R"); // рисуем точку красным цветом
text1(ctx, "O3", O3, "rt", "up", "R"); // обозначаем точку как "O3" красным цветом
circle(ctx, O3, R3, 1, "R"); // рисуем окружность красным цветом
// с центром в точке O3 и радиусом равным R3
// Проверяем пересекаются или нет окружность
// cir2 с сопрягающей окружностью cir3
// Координаты двух точек пересечения полученные в результате
// работы функции Intersection_TwoCircles должны
// отличаться совершенно незначительно по своим значениям
// и в пределе переходить в одну точку касания окружностей "G".
points = cir2.Intersection_TwoCircles(cir3);
if (points == null)
{
return null;
}
// Первая точка "G" сопряжения/касания
var G = new Point2D(); // объявление точки
G[0] = points[0][0];
G[1] = points[0][1];
csp(ctx, G, 3, "R"); // рисуем точку красным цветом
text1(ctx, "G", G, "lt", "dn", "R"); // обозначаем точку как "G"
// Проверяем пересекаются или нет окружность
// cir1 с сопрягающей окружностью cir3
// Координаты двух точек пересечения полученные в результате
// работы функции Intersection_TwoCircles должны
// отличаться совершенно незначительно по своим значениям
// и в пределе переходить в одну точку касания окружностей "F".
points = cir1.Intersection_TwoCircles(cir3);
if (points == null)
{
return null;
}
// Вторая точка "F" сопряжения/касания
var F = new Point2D(); // объявление точки
F[0] = points[0][0];
F[1] = points[0][1];
csp(ctx, F, 3, "R"); // рисуем точку красным цветом
text1(ctx, "F", F, "lt", "dn", "R"); // обозначаем точку как "F"
// Предварительные расчеты требующиеся для рисования дуги сопряжения.
// Вычисляем углы начала и конца дуги сопряжения.
var line_O3_F = new Line2D(O3, F);
var line_O3_G = new Line2D(O3, G);
var line_hor = new Line2D(O3, new Point2D(O3[0] + 1, O3[1]));
var ang_F_degree = (180 / Math.PI) * line_O3_F.Angle(line_hor);
var ang_G_degree = (180 / Math.PI) * line_O3_G.Angle(line_hor);
// Рисуем "жирную" дугу сопряжения окружностей красным цветом
arc(ctx, O3, R3, 4, "R", -ang_G_degree, -ang_F_degree);
}
Полный текст программы сопряжения окружностей с отрисовкой на холсте находится в файле three_circles.js.
Рассмотрим построение правильных многоугольников на холсте. Простейший способ таких построений состоит в делении окружности на соответствующее количество частей при помощи транспортира и соединении между собой получившихся точек.
Однако эти построения можно провести только при помощи циркуля и линейки. В книге Джона Аллена "Базовые геометрические формы для дизайнеров и архитекторов" (издательство Питер 2016г.) подробно рассматриваются такие построения. Воспользуемся этой книгой и построим пятиугольник (pentagon), шестиугольник (hexagon) и семиугольник (heptagon). Только в качестве циркуля (как это делается в книге) будем использовать функцию создания окружности, а в качестве линейки (она используется в книге) - функцию создания прямой из библиотеки WebGeometry. Начнем с пятиугольника.
Начертим окружность с центром в точке O. Проведем горизонтальный диаметр окружности и получим точки
пересечения A и B. В книге эти точки просто отмечаются карандашом, а мы используем для этого
функцию Intersection_LineCircle
из библиотеки WebGeometry. Раствором циркуля равным радиусу исходной окружности из точки B
проведем дугу (вместо дуг при вычислениях используем функции Circle2D)
пересекающую окружность в точках C и D. Соединим точки C и D
чтобы найти точку E, делящую отрезок OB на две равные части.
Затем проводим вертикальную ось через точку O и пересекающую окружность в точке F.
Установив ножку циркуля в точке E, раствором циркуля, равным EF, проведем дугу, пересекающую
горизонтальную ось в точке G. Установив ножку циркуля в точке F, раствором циркуля, равным FG,
проведем дугу пересекающую окружность в точках H и J. Из точек H и J проведем дуги, используя
тот же раствор циркуля, чтобы найти точки K и L. FJKLH - искомый пятиугольник.
Точки пересечения дуг окружностей определяются с помощью функции
Intersection_TwoCircles
Исходный текст программы построения пятиугольника приведен в файле pentagon.js.
Перейдем к построению правильного шестиугольника.
Начертим произвольную окружность с центром в точке O и радиусом OA равным значению R.
В качестве точки A может быть выбрана произвольная точка лежащая на окружности.
Установив ножку циркуля в точке A и используя тот же самый радиус проведем через центр O
дугу BC (от одной стороны окружности до другой). Из точки B проведем дугу через точки A,
O и новую точку D на окружности. Таким же образом из точки D проведем еще одну
дугу от точки B, чтобы найти точку E.
Далее продолжаем рисовать дуги из точек E, F и C,
пока не получится шестиугольник ABDEFC.
Исходный текст программы построения шестиугольника приведен в файле hexagon.js. При расчетах его
вершин координаты точек пересечения дуг между собой мы опредеделяем при помощи
функции Intersection_TwoCircles
входящей в состав библиотеки WebGeometry, а рисуем дуги на холсте
используя функцию arc из файла canvas2D.js. Эта функция сделана на основе одноименной
функции arc входящей в HTML5 Canvas.
Построим почти правильный семиугольник. Как пишет (в упомянутой выше книге) Джон Аллен это построение точно на 99.9%.
Начертим произвольный круг с центром в точке O и радиусом OC равным значению R.
Построим квадрат EFGH вокруг этого круга. Из точек E и F проведем две дуги, имеющие радиус,
равный отрезку EF, и пересекающиеся в точке J внутри квадрата. EFJ - равносторонний треугольник,
пересекающий изначальную окружность в точках K и L. CK и CL можно считать сторонами правильного
семиугольника с точностью 99.9%.
Установив раствор циркуля равным CK и двигаясь по окружности начиная из точки K,
отметим остальные четыре точки семиугольника. В результате получится семиугольник CKMNPQL.
Исходный текст программы построения семиугольника приведен в файле heptagon.js.